Organisers:
Warwick Tucker (Monash University)
Andy Hammerlindl (Monash University)
Hinke Osinga (University of Auckland)
Bernd Krauskopf (University of Auckland)

Program Description:

The main aim of the research program is to make a breakthrough in the problem of searching for, approximating, and proving the existence of special dynamical objects called blenders.

The structure of the event will be to have two hours of talks each morning and leave the rest of the day to informal discussion. We will have three mini-courses, each consisting of four lectures, and five stand-alone talks. We will also dedicate three hours for all participants to give brief presentations of themselves and their current projects. The goal of these mini-courses and lectures are to bring participants up to speed in the latest advancements in relevant fields, and to foster the topics of discussion.

The mini-courses have been chosen to closely align with the research aims of the event and are as follows:
(1) An introduction to blenders – Lorenzo Díaz
(2) Computational invariant manifolds – Hinke Osinga and Bernd Krauskopf
(3) Computer-aided proofs in dynamics — Maciej Capiński

Topic 1: Blenders A blender is a compact, invariant set on which a diffeomorphism has a certain behavior. This behavior forces topologically thin sets to intersect in a robust way, producing rich dynamics. The term blender describes its function: to blend together stable and unstable manifolds. Blenders have been used to construct diffeomorphisms with surprising properties and have played an important role in the classification of smooth dynamical systems. One of the original applications of blenders is also one of the more striking. A diffeomorphism g of a compact manifold is robustly transitive if there exists a point whose orbit is dense in the manifold, and moreover this property persists when g is slightly perturbed. Until the 1990s there were no known
robustly transitive diffeomorphisms in the isotopy class of the identity map on any manifold. Bonatti and Díaz (Ann. of Math., 1996) used blenders to construct robustly transitive diffeomorphisms as perturbations of the identity map on certain 3-manifolds.

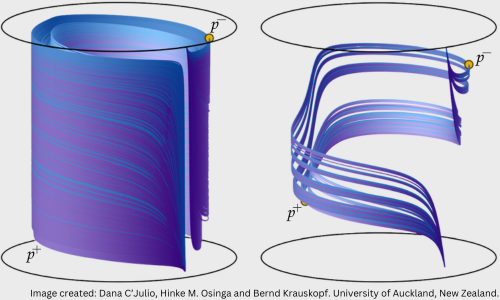
Topic 2: Computational invariant manifolds Global invariant manifolds play an important role in organising the behaviour of a dynamical system. Together with equilibria and periodic orbits, they form the so-called skeleton of the dynamics and offer geometric insight into how observed behaviour arises. In most cases, it is impossible to find invariant manifolds explicitly and numerical methods must be used to find accurate approximations. Developing such computational techniques is a challenge on its own and, to this date, the focus has primarily been on computing two-dimensional manifolds. Nevertheless, these computational efforts offer new insights that go far beyond a confirmation of the known theory. Furthermore, global invariant manifolds in dynamical systems theory not only explain asymptotic behaviour, but more recent developments show that they are equally useful for explaining short-term transient dynamics.

Topic 3: Computer-aided proofs in dynamics In recent years computer-aided proofs in mathematical analysis have gained increasing presence in mathematical research. The main reason for the growing impact of this area is its ability to produce high-quality quantitative information about global, nonlinear problems. As a result, solutions to a large class of previously intractable problems are now within reach. Since the turn of the century, several long-standing conjectures in pure mathematics have been verified using rigorous computations. Having access to different levels of rigour (approximations, computer-aided proofs, formal proofs) will play an instrumental role for mathematical research that deals with highly nonlinear problems such as those addressed in this research program.

Program Structure:

Click here to view the recording of the talks

Participant List
Warwick Tucker (Monash University)
Andy Hammerlindl (Monash University)
Hinke Osinga (University of Auckland)
Bernd Krauskopf (University of Auckland)
Maciej Capiński (AGH University of Krakow)
Lorenzo J. Diaz (PUC-Rio)
Holger Dullin (University of Sydney)
Gary Froyland (UNSW Sydney)
Zbigniew Galias (AGH University in Krakow)
Cecilia Gonzalez Tokman (University of Queensland)
Mioara Joldes (CNRS, LAAS-CNRS, France)
Hiroshi Kokubu (Kyoto University)
Courtney Quinn (University of Tasmania)
Theodore Vo (Monash University)
Juan Patino (University of Auckland)
Sam Doak (University of Auckland)
Sakshi Jain (Monash University)
Yovani Herrera (Monash University)
Marisa Cantarino (Monash University)
Andrew Cook (Monash University)
Natalia McAlister (Monash University)
Hiroe Oka (Ryukoku University)
Katrin Gelfert (Universidade Federal do Rio de Janeiro)

ASSOCIATED EVENTS
MATRIX Wine and Cheese Afternoon 6 Feb 2024
On the first Tuesday of each program, MATRIX provides a pre-dinner wine and cheese afternoon. Produce is locally-sourced to showcase delicacies from the region.