Organisers:
Eleonora Cinti (Universita di Bologna)
Armin Schikorra (University of Pittsburgh)
Enrico Valdinoci (University of Western Australia)

Program Description:
The study of minimal surfaces, surfaces of constant mean curvature, curve-shortening flows, mean curvature flows, Gauss curvature flows, etc. are classical topics in the field of geometric analysis. Their understanding requires combined methods from mathematical analysis and differential geometry, and the results obtained have important applications in several directions, including phase transitions, moving fronts, free boundary problems, and mathematical biology.

As a counterpart, in the recent years there has been a surge of interest in the study of nonlocal minimal surfaces and nonlocal geometric flows. The notion of nonlocal perimeter has applications and connections with several fields, such as long-range phase coexistence models, spin models in statistical mechanics, geometric flows, image reconstruction and nonlocal capillarity models.

This event brings together experts in the study of classical and nonlocal geometric problems, to exchange their knowledge and techniques, and train PhD Students and Early Career Researchers with the objective of solving important and high impact research questions. Special interest is devoted to the study of classification and regularity results for classical and nonlocal minimal surfaces and existence and qualitative properties of solutions to classical and nonlocal geometric flows.

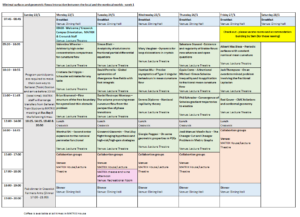
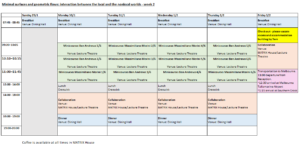
Program Structure:

Participants List:
Enrico Valdinoci (University of Western Australia)
Armin Schikorra (University of Pittsburgh)
Jack Thompson (University of Western Australia)
Giovanni Giacomin (University of Western Australia)
Cristiana De Filippis (University of Parma)
Mary Vaughan (University of Texas at Austin)
José Manuel Mazón Ruiz (Universitat de Valencia)
Simon Blatt (Paris-Lodron University Salzburg)
Massimiliano Morini (University of Parma)
Serena Dipierro (University of Western Australia)
Ben Andrews (Australian National University)
Giorgio Poggesi (University of Western Australia)
Wenhui Shi (Monash University)
Haotian Wu (University of Sydney)
David Perrella (University of Western Australia)
Albert Mas Blesa (Universitat Politècnica de Catalunya)
Daniel Restrepo Montoya (University of Texas at Austin)
Gyula Csato (University of Barcelona)
Philip Schrader (University of Western Australia)
Rod Gover (University of Auckland)
Valentina Wheeler (SMAS/ University of Wollongong)
Salvatore Stuvard (University of Milan)
Brian Krummel (University of Melbourne)
Tal Gurfinkel (University of Western Australia)
Sathyanarayanan Rengaswami (University of Tennessee)
Chrisopher Hopper (University of Newcastle)

Registration is closed

ASSOCIATED EVENTS
MATRIX Wine and Cheese Afternoon 24 January 2023
On the first Tuesday of each program, MATRIX provides a pre-dinner wine and cheese afternoon. Produce is locally-sourced to showcase delicacies from the region.